|
|
|
| Title | Puzzle: find the equilateral triangles in Visual Basic 6 |
|---|
| Description | This example describes a puzzle to find the equilateral triangles in Visual Basic 6. |
|---|
| Keywords | algorithms, games, graphics, mathematics, example, example program, Windows Forms programming, Visual Basic 6, VB 6 |
|---|
| Categories | Graphics, Graphics, Algorithms, Puzzles and Games |
|---|
|
|
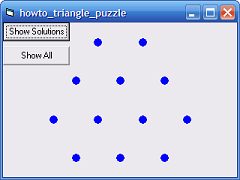
This is a puzzle that was used recently on National Public Radio (NPR). How many equilateral triangles can you make with corners on the points drawn by the program? For this blog, the puzzle has two parts. First see if you can solve the puzzle "manually." Then write a program that solves the puzzle.
The code available for download with this post draws the points and will draw the solution after you fill in the appropriate code. You only need to fill in a small piece of code that initializes the solution, or better yet discovers the solution for you.
The rest of this post shows how parts of the program that I've written for you work. The following code executes when the form loads. (This is where you need to add your code.)
|
|
' The points.
Private Xs As Collection
Private Ys As Collection
' The solutions.
Private Solutions As Collection
' The solution we should display.
Private CurrentSolution As Integer
' Define the points and solutions.
Private Sub Form_Load()
Dim dy As Single
Dim dx As Single
Dim top_x As Single
Dim top_y As Single
ScaleMode = vbPixels
' Define the points.
dy = CSng(ScaleHeight / 4)
dx = CSng(dy / Sqr(3))
top_x = CSng(ScaleWidth / 2)
top_y = -dy / 2
Set Xs = New Collection
Set Ys = New Collection
Xs.Add (top_x - dx): Ys.Add (top_y + dy)
Xs.Add (top_x + dx): Ys.Add (top_y + dy)
Xs.Add (top_x - 2 * dx): Ys.Add (top_y + 2 * dy)
Xs.Add (top_x - 0 * dx): Ys.Add (top_y + 2 * dy)
Xs.Add (top_x + 2 * dx): Ys.Add (top_y + 2 * dy)
Xs.Add (top_x - 3 * dx): Ys.Add (top_y + 3 * dy)
Xs.Add (top_x - 1 * dx): Ys.Add (top_y + 3 * dy)
Xs.Add (top_x + 1 * dx): Ys.Add (top_y + 3 * dy)
Xs.Add (top_x + 3 * dx): Ys.Add (top_y + 3 * dy)
Xs.Add (top_x - 2 * dx): Ys.Add (top_y + 4 * dy)
Xs.Add (top_x - 0 * dx): Ys.Add (top_y + 4 * dy)
Xs.Add (top_x + 2 * dx): Ys.Add (top_y + 4 * dy)
' Define the solutions.
Set Solutions = New Collection
' Insert your code here...
AddSolution 1, 3, 4
' Start displaying no solution.
CurrentSolution = Solutions.Count + 1
End Sub
|
|
|
This code creates the Xs and Ys collections that hold the coordinates of the points and defines the points. The points are numbered from top to bottom and left to right so the points in the first row have indices 1 and 2, the points in the second row have indices 3, 4, and 5, and so forth.
This code also creates the Solutions collection. Your code should add collections holding three integers each to the Solutions collection to indicate the indices of points that make up the triangles. To make this easier, the program includes the following AddSolution subroutine that adds a triangle to thue solution. The Form_Load event handler calls AddSolution once to show how to create a triangle that uses the points numbered 1, 3, and 4.
|
|
' Add a new solution.
Private Sub AddSolution(ParamArray indices() As Variant)
Dim new_solution As Collection
Dim i As Integer
' Create the new solution collection.
Set new_solution = New Collection
For i = LBound(indices) To UBound(indices)
new_solution.Add indices(i)
Next i
' Add the new solution to the solutions list.
Solutions.Add new_solution
End Sub
|
|
|
The AddSolution subroutine creates a new collection to hold the new solution. It loops through the parameters passed to the routine adding them to the new collection. It then adds that collection to the Solutions collection.
The program uses the following Paint event handler to draw the points and the solution triangle indicated by the CurrentSolution variable.
|
|
' Draw the circles and any triangles currently defined.
Private Sub Form_Paint()
Const radius As Single = 5
Dim i As Integer
' Draw the points.
Me.FillStyle = vbFSSolid
Me.FillColor = vbBlue
For i = 1 To Xs.Count
Me.Circle (Xs(i), Ys(i)), radius, vbBlue
Next i
' Draw the current solution.
If (CurrentSolution < 1) Then
' Draw all solutions.
For i = 1 To Solutions.Count
DrawSolution i
Next i
Else
' Draw the current solution.
DrawSolution CurrentSolution
End If
End Sub
|
|
|
This code loops through the point coordinates and draws the points. Then if CurrentSolution is less than 1, the program loops through all of the solutions and calls DrawSolution for each. If CurrentSolution is not less than 1, the program calls DrawSolution to draw just that solution.
The following code shows how the DrawSolution method draws a particular solution.
|
|
' Draw a solution.
Private Sub DrawSolution(ByVal solution_num As Integer)
Dim solution As Collection
Dim i As Integer
If (solution_num > Solutions.Count) Then Exit Sub
' Draw this solution.
Set solution = Solutions(solution_num)
' Start at the last point.
Me.CurrentX = Xs(solution(solution.Count))
Me.CurrentY = Ys(solution(solution.Count))
' Connect to the other points.
For i = 1 To solution.Count
Me.Line -(Xs(solution(i)), Ys(solution(i))), vbRed
Next i
End Sub
|
|
|
If the solution number passed to the method is not a valid solution index, the method returns without doing anything.
If the solution number is valid, the code sets the form's CurrentX and CurrentY properties to the lastg point in the current solution. It then loops through the points in the solution drawing a line connecting them to the previous point.
The rest of the program's code is reasonably straightforward.
|
|
' Start showing solutions.
Private Sub cmdShowSolutions_Click()
' Disable the button.
cmdShowSolutions.Enabled = False
' Start at the first solution.
CurrentSolution = 1
' Start the timer.
tmrChangeSolution.Enabled = True
' Redraw.
Refresh
End Sub
' Show the next solution.
Private Sub tmrChangeSolution_Timer()
' Increment CurrentSolution. If the result is greater
' than the
' last solution's index, disable the timer.
CurrentSolution = CurrentSolution + 1
tmrChangeSolution.Enabled = (CurrentSolution <= _
Solutions.Count)
' If we're done drawing, enable the button.
cmdShowSolutions.Enabled = (Not _
tmrChangeSolution.Enabled)
' Redraw.
Refresh
End Sub
' Show all of the solutions.
Private Sub cmdShowAllSolutions_Click()
CurrentSolution = 0
tmrChangeSolution.Enabled = False
cmdShowSolutions.Enabled = True
Refresh
End Sub
|
|
|
When you click the Show Solutions button, the program disables that button so you can't press it again. It then sets CurrentSolution = 1 to display the first solution, enables the tmrChangeSolution Timer, and refreshes the form to redraw. The Paint event handler draws the selected solution (number 1). If there are no solutions, then the DrawSolution method draws nothing because the index 1 is not a valid index in the Solutions list.
When the timer ticks, the program increments CurrentSolution. It sets the Timer's Enabled property to true if the new value is still a valid solution index so the Timer runs until the last solution has been displayed. If the timer is no longer enabled, the code re-enables the Show Solutions button. The Tick event handler finishes by refreshing the form to redraw it.
Finally if when you click the Show All button, the program sets CurrentSolution to 0 and refreshes to redraw the solution. If you look back at the Paint event handler, you'll see that it calls DrawSolution for every solution if CurrentSolution < 1.
Download the example program and try to solve the puzzle. You can explicitly enter code to create solutions that you figured out yourself, or you can write code to find all of the solutions. Here's a small hint: There are more solutions than you will probably think of at first.
If you find a solution, zip up your project and email it to me. I'll post my solutions (manually solved and automatically solved) and any others that I receive on Monday and Tuesday, November 28 and 29, 2011.
Related links:
|
| |
|
|
| |
| |
 |
| |
|
|
