Cartographers have always know that you can color any map using four colors so any two regions that share an edge have different colors. In 1852 Francis Guthrie asked if this could be proven. After more than 100 years and several false starts, Appel and Haken proved the four-color theorem in 1976. The proof required a computer to exhaustively examine more than 1,700 different map configurations. More recently Robertson, Sanders, Seymour, and Thomas published a new proof using only 633 map configurations.

There are also some interesting results for other number of colors.

Two-coloring a map is easy. Assign a color to one region. Then give its neighors the other color. Give their neighbors the first color, and so on until you either finish coloring every region. If at any point two adjacent regions having the same color, the map is not two-colorable.

Three-coloring a map is NP-complete. There is no polynomial time method for even determining whether a map is three-colorable, much less finding a two-coloring. One method is to exhaustively try every possible combination of colors for the regions. If you have N regions, that means trying 3^N arrangements. For example, to color the 48 contiguous US states you would need to examine roughly 8e22 combinations. There are some techniques for simplifying the map before you color it. For example, if a region has two or fewer neighbors, remove it and color the rest of the map first. Then replace the region and give it one of the colors not used by its neighbors.

The four-coloring proofs show how to find a valid four coloring but the huge number of cases to check makes them difficult to implement in practice. There are tricks similar to those you can use for three-coloring to cimplify the map, but in the end you may need to search some color combinations exhaustively.

Exercises

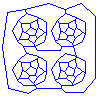
1. Find a valid four-coloring of this map.
2. Find a valid four-coloring of this map. In 1975 Martin Gardner claimed that this map could not be four-colored as an April Fool's joke.

Five-coloring a map isn't easy but it is relatively fast. There is an algorithm that simplifies the map until there are no regions left. It then restores the regions one by one, assigning them correct colors. (I may post an outline of the algorithm later if I have time.)

Links

Believe it or not, there is also a book about the four-color theorem titled appropriately enough The Four-Color Theorem. [Amazon.com] [Amazon.co.uk]

Solutions to Exercises

1. Solution for map 1.
2. Solution for map 2.