|
|
|
| Title | Find a polynomial least squares fit for a set of points in Visual Basic 6 |
|---|
| Description | This example shows how to find a polynomial least squares fit for a set of points in Visual Basic 6. |
|---|
| Keywords | algorithms, mathematics, least squares, polynomial least squares, curve fitting, graphics, Visual Basic 6, VB 6 |
|---|
| Categories | Algorithms, Algorithms, Graphics, Graphics |
|---|
|
|
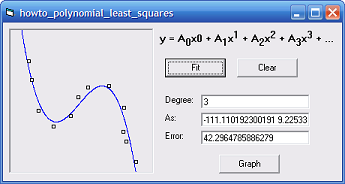
(This is pretty confusing but you can get through it if you take it one step at a time.)
The example Find a linear least squares fit for a set of points in Visual Basic 6 explains how to find a line that best fits a set of data points. If you haven't read that example yet, do so now because this example follows the same basic strategy.
With a degree d polynomial least squares fit, you want to find the coefficients A0, A1, ... Ad to make the following equation fit the data points as closely as possible:
A0 * x0 + A1 * x1 + A2 * x2 + ... + + Ad * xd
The goal is to minimize the sum of the squares of the vertical distances between the curve and the points.
Keep in mind that you know all of the points so for given coefficients you can easily loop through all of the points and calculate the error.
If you store the coefficients in a List(Of Double), then the following function calculates the value of the function F(x) at the point x.
|
|
' The function.
Public Function F(ByVal coeffs As Collection, ByVal x As _
Double) As Double
Dim total As Double
Dim x_factor As Double
Dim i As Integer
total = 0
x_factor = 1
For i = 1 To coeffs.Count
total = total + x_factor * coeffs(i)
x_factor = x_factor * x
Next i
F = total
End Function
|
|
|
The following function uses the function F to calculate the total error squared between the data points and the polynomial curve.
|
|
' Return the error squared.
Public Function ErrorSquared(ByVal PtX As Collection, ByVal _
PtY As Collection, ByVal coeffs As Collection) As Double
Dim total As Double
Dim pt As Integer
Dim dy As Double
total = 0
For pt = 1 To PtX.Count
dy = PtY.Item(pt) - F(coeffs, PtX.Item(pt))
total = total + dy * dy
Next pt
ErrorSquared = total
End Function
|
|
|
The following equation shows the error function:
![Sum[(yi - (A0 * x^0 + A1 * x^1 + A2 * x^2 + ... + Ad*x^d)^2]](howto_polynomial_least_squares_eq1.png)
To simplify this, let Ei be the error in the ith term so:
![Sum[(Ei)^2]](howto_polynomial_least_squares_eq2.png)
The steps for finding the best solution are the same as those for finding the best linear least squares solution:
- Take the partial derivatives of the error function with respect to the variables, in this case A0, A1, ... Ad.
- Set the partial derivatives equal to 0 to get N + 1 equations and N + 1 unknowns A0, A1, ... Ad.
- Solve the equations for A0, A1, ... Ad.
As was the case in the previous example, this may sound like an intimidating problem. Fortunately the partial derivatives of the error function are simpler than you might think because that function only involves simple powers of the As. For example, the partial derivative with respect to Ak is:
![Sum[2 * Ei * partial(Ei, Ak)]](howto_polynomial_least_squares_eq3.png)
The partial derivative of Ei with respect to Ak contains lots of terms involving powers of xi and different As, but with respect to Ak all of those are constants except the single term Ak * xik. All of the other terms drop out leaving:
![Sum[2 * Ei * (-xi^k)]](howto_polynomial_least_squares_eq4.png)
If you substitute the value of Ei, multiply the -xik term through, and add the As separately you get:
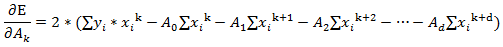
As usual, this looks pretty messy, but if you look closely you'll see that most of the terms are values that you can calculate using the xi and yi values. For example, the first term is simply the sum of the products of the yi values and the xi values raised to the kth power. The next term is A0 times the sum of the xi values raised to the kth power. Because the yi and xi values are all known, this equation is the same as the following for a particular set of constants S:
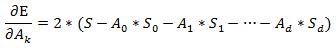
This is a relatively simple equation with d + 1 unknowns A0, A1, ..., Ad.
When you take the partial derivatives for the other values of k as k varies from 0 to d, you get d + 1 equations with d + 1 unknowns, and you can solve for the unknowns.
Linear least squares is a specific case where d = 1 and it's easy to solve the equations. For the more general case, you need to use a more general method such as Gaussian elimination. The example Solve a system of equations with Gaussian elimination in VB 6 explains how Gaussian elimination works, but for now assume you have code that can perform Gaussian elimination to solve for the As.
The following code shows how the example program finds polynomial least squares coefficients.
|
|
' Find the least squares linear fit.
Public Function FindPolynomialLeastSquaresFit(ByVal PtX As _
Collection, ByVal PtY As Collection, ByVal degree As _
Integer) As Collection
Dim j As Integer
Dim pt As Integer
Dim a_sub As Integer
Dim coeff As Variant
' Allocate space for (degree + 1) equations with
' (degree + 2) terms each (including the constant term).
Dim coeffs() As Double
Dim answer() As Double
ReDim coeffs(degree, degree + 1)
' Calculate the coefficients for the equations.
For j = 0 To degree
' Calculate the coefficients for the jth equation.
' Calculate the constant term for this equation.
coeffs(j, degree + 1) = 0
For pt = 1 To PtX.Count
coeffs(j, degree + 1) = coeffs(j, degree + 1) - _
(PtX.Item(pt) ^ j) * PtY.Item(pt)
Next pt
' Calculate the other coefficients.
For a_sub = 0 To degree
' Calculate the dth coefficient.
coeffs(j, a_sub) = 0
For pt = 1 To PtX.Count
coeffs(j, a_sub) = coeffs(j, a_sub) - _
PtX.Item(pt) ^ (a_sub + j)
Next pt
Next a_sub
Next j
' Solve the equations.
answer = GaussianElimination(coeffs)
' Return the result converted into a Collection.
Set FindPolynomialLeastSquaresFit = New Collection
For Each coeff In answer
FindPolynomialLeastSquaresFit.Add CDbl(coeff)
Next coeff
End Function
|
|
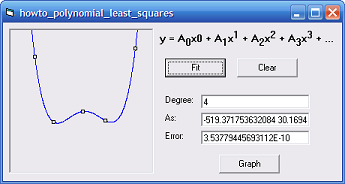
The code simply builds an array holding the coefficients (the Ss in the previous equation) and then calls the GaussianElimination method to find the As. It converts the result from an array into a List(Of Double) for convenience and returns it.
Give the program a try. It's pretty cool!
Tip: Use the smallest degree that makes sense for your problem. If you use a very high degree, the curve will fit the points very closely but it will probably emphasize structure that isn't really there. For example, the picture on the right fits a degree 4 polynomial to points that really should be fit with a degree 2 polynomial.
|
| |
|
|
| |
| |
 |
| |
|
|
