Good examples of recursion are hard to come by because the human brain normally thinks iteratively. For example, if you need to paint a fence, you probably think about starting at one end and working your way to the other. You probably don't think it terms of dividing the fence into two pieces and recursively painting each.

The Tower of Hanoi problem is a problem with a good, naturally recursive solution.

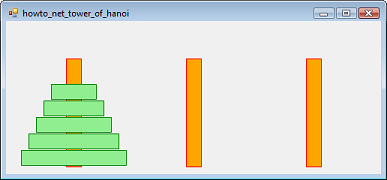
Consider the three pegs shown in the figure. The goal is to move the pile of green disks from the left orange peg to another (say the middle peg). You can only move one disk at a time and you can never place a big disk on a smaller disk.

Figuring out how to do this directly is tricky but there is a simple recursive solution. First recursively move every disk except the bottom one to the unused peg (in this case, the right peg). Now there is only one disk on the left peg and no disks on the middle peg so you can move the remaining disk there. Now recursively move the remaining disks from the right peg to the middle peg.

If that's too confusing, consider a smaller problem with only two disks. To move them from the left to middle peg, first move the top disk to the right peg. Then move the bottom disk to the middle peg. Finally move the top disk to the middle peg. Run the program a few times to see how it works for the larger problem. You can adjust the Delay constant to make the program run slower or faster.

The program stores information about the disks in Stacks. The Stack class provides a Push method to add something and a Pop method for removing the most recently added item. The program uses Stacks so it can only add and remove disks from the tops of the pegs. (No sneaking one out of the middle!)

The OccupiedPegNum variable keeps track of the Stack that holds all of the disks (when they are not moving).

' Peg stacks. Each disk is represented by its width.
Private PegStack(3) As Stack(Of Integer)

' The peg that currently holds the disks.
Private OccupiedPegNum As Integer = 0

' Move num_disks disks from peg from_peg to peg to_peg.
Private Sub MoveDisks(ByVal from_peg As Integer, ByVal _
    to_peg As Integer, ByVal other_peg As Integer, ByVal _
    num_disks As Integer)
    ' See if we have more than one disk to move.
    If (num_disks > 1) Then
        ' We have more than one disk to move.
        ' Recursively move all but one disk to the other
        ' peg.
        MoveDisks(from_peg, other_peg, to_peg, num_disks - _
            1)
    End If

    ' Move the remaining disk.
    PegStack(to_peg).Push(PegStack(from_peg).Pop())
    Me.Refresh()
    System.Threading.Thread.Sleep(Delay)

    If (num_disks > 1) Then
        ' Recursively move the other disks back where they
        ' belong.
        MoveDisks(other_peg, to_peg, from_peg, num_disks - _
            1)
    End If
End Sub

Experiment with the program a bit to see how it works.