Suppose you have a set of data points that you believe were generated by a process that should ideally be linear. In that case, you might like to find the best parameters m and b to make the line y = m * x + b fit those points as closely as possible.

A common approach to this problem is to minimize the sum of the squares of the vertical distances between the line and the points. For example, suppose the point P0 = (x0, y0) is one of your data points. The vertical error squared for that point is the difference between y0 and the line's Y coordinate for that X position. In this case, that's y0 - (m * x0 + b). To calculate the total error squared, square this error and add up the errors squared for all of the points.

Keep in mind that you know all of the points so for given values of m and b you can easily loop through all of the points and calculate the error.

' Return the error squared.
Public Function ErrorSquared(ByVal points As List(Of _
    PointF), ByVal m As Double, ByVal b As Double) As Double
    Dim total As Double = 0
    For Each pt As PointF In points
        Dim dy As Double = pt.Y - (m * pt.X + b)
        total += dy * dy
    Next pt
    Return total
End Function

As a mathematical equation, the error function E is:

where the sum is performed over all of the points (x_i, y_i).

To find the least squares fit, you need to minimize this function E(m, b). That sounds intimidating until you remember that the x_i and y_i values are all known--they're the values you're trying to fit with the line.

The only variables in this equation are m and b so it's relatively easy to minimize this equation by using a little calculus. Simply take the partial derivatives of E with respect to m and b, set the two resulting equations equal to 0, and solve for m and b.

Taking the partial derivative with respect to m and rearranging a bit to gather common terms and pull constants out of the sums you get:

Taking the partial derivative with respect to b and rearranging a bit you get:

To find the minimum for the error function, you set these two equations equal to 0 and solve for m and b.

To make working with the equations easier, let:

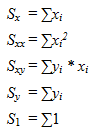
If you make these substitutions and set the equations equal to 0 you get:

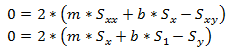
Solving for m and b gives:

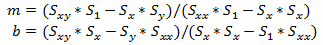
Again these look like intimidating equations but all of the S's are values that you can calculate given the data points that you are trying to fit.

The following code calculates the S's and uses them to find the linear least squares fit for the points in a List(Of PointF).

' Find the least squares linear fit.
' Return the total error.
Public Function FindLinearLeastSquaresFit(ByVal points As _
    List(Of PointF), ByRef m As Double, ByRef b As Double) _
    As Double
    ' Perform the calculation.
    ' Find the values S1, Sx, Sy, Sxx, and Sxy.
    Dim S1 As Double = points.Count
    Dim Sx As Double = 0
    Dim Sy As Double = 0
    Dim Sxx As Double = 0
    Dim Sxy As Double = 0
    For Each pt As PointF In points
        Sx += pt.X
        Sy += pt.Y
        Sxx += pt.X * pt.X
        Sxy += pt.X * pt.Y
    Next pt

    ' Solve for m and b.
    m = (Sxy * S1 - Sx * Sy) / (Sxx * S1 - Sx * Sx)
    b = (Sxy * Sx - Sy * Sxx) / (Sx * Sx - S1 * Sxx)

    Return Math.Sqrt(ErrorSquared(points, m, b))
End Function