|
|
|
| Title | Draw a Mandelbrot set with smoothly shaded colors in Visual Basic 6 |
|---|
| Description | This example shows how to draw a Mandelbrot set with smoothly shaded colors in Visual Basic 6 |
|---|
| Keywords | graphics, fractals, Mandelbrot, Mandelbrot set, algorithms, complex, complex numbers, iterated system, iteration, Visual Basic 6, VB6 |
|---|
| Categories | Graphics, Algorithms, Graphics |
|---|
|
|

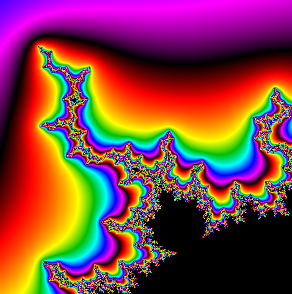




You may not have heard that Benoît Mandelbrot (November 20, 1924 - October 14, 2010) recently passed away. In his honor, I decided to enhance the Mandelbrot set program shown in an earlier example. For more information on Benoît Mandelbrot, see Wikipedia or his New York Times obituary.
The example Use a Complex class to draw the Mandelbrot set easily in Visual Basic 6 explains how to draw a Mandelbrot set by iterating the equation:
Zn = Zn-12 + C
Where Zn and C are complex numbers. The program iterates this equation until the magnitude of Zn is at least 2 or the program performs a maximum number of iterations. At that point it uses the number of iterations to determine a color for the pixel. If the program performed num_iterations iterations and is using num_colors colors, then the program colors the pixel Colors[num_iterations % num_colors].
This example modifies the coloring algorithm to produce smoothly varying colors. First note that the following value mu approximates the fractional number of iterations that would be needed before the magnitude of Zn is at least 2.
mu = iteration + 1 - Log(Log(Z.Magnitude)) / log_escape
Here iteration is the number of iterations actually performed, Z.Magnitude is the magnitude of Z right after the magnitude is greater than 2, and log_escape is the logarithm of the escape radius 2.
This value only approximates the actual expected fractional number of iterations and there is a noticeable error where the colors don't blend smoothly. Fortunately it's easy to reduce the error by using a later value of Zn. For example, if you use Zn+3, then the error isn't noticeable. The following shows the code used by the program to calculate mu.
|
|
' Reduce the error in mu.
For i = 0 To 2
Set Z = Z.Times(Z).Plus(C)
iteration = iteration + 1
Next i
mu = iteration + 1 - _
Log(Log(Z.Magnitude)) / log_escape
|
|
|
This program also provides one other smooth color model. If you use the second smooth model in the configuration form, the program scales the resulting value of mu so it varies only once over the available colors as the number of iterations varies from 0 to the maximum number of iterations. That means the colors do not repeat and you get a very gradual smoothing.
|
|
If mnuColorsSmooth2.Checked Then
mu = mu / MaxIterations * NumColors
End If
|
|
|
Finally after calculating mu with whichever method, the code calls GetColor to return an appropriate color for the pixel.
|
|
' Get a color for this pixel.
Private Function GetColor(ByVal mu As Double) As OLE_COLOR
Dim clr1 As Integer
Dim clr2 As Integer
Dim t2 As Double
Dim t1 As Double
Dim r1 As Byte
Dim g1 As Byte
Dim b1 As Byte
Dim r2 As Byte
Dim g2 As Byte
Dim b2 As Byte
Dim r As Integer
Dim g As Integer
Dim b As Integer
clr1 = CInt(Int(mu))
t2 = mu - clr1
t1 = 1 - t2
clr1 = clr1 Mod NumColors
clr2 = (clr1 + 1) Mod NumColors
UnRGB Colors(clr1), r1, g1, b1
UnRGB Colors(clr2), r2, g2, b2
r = CInt(r1 * t1 + r2 * t2)
g = CInt(g1 * t1 + g2 * t2)
b = CInt(b1 * t1 + b2 * t2)
GetColor = RGB(r, g, b)
End Function
' Return a color's red, green, and blue components.
Private Sub UnRGB(ByRef color As OLE_COLOR, ByRef r As Byte, _
ByRef g As Byte, ByRef b As Byte)
r = color And &HFF&
g = (color And &HFF00&) \ &H100&
b = (color And &HFF0000) \ &H10000
End Sub
|
|
|
The GetColor method truncates mu to find an integer color index value and a fractional value. It then returns a color that uses the weighted average of the integer color and the following color.
See the code for additional details.
|
| |
|
|
| |
| |
 |
| |
|
|
