|
|
|
| Title | Find the tangent lines between two circles in Visual Basic 6 |
|---|
| Description | This example shows how to find the tangent lines between two circles in Visual Basic 6. |
|---|
| Keywords | tangents, circle, tangent lines, geometry, graphics, algorithms, Visual Basic 6, VB 6 |
|---|
| Categories | Algorithms, Graphics |
|---|
|
|
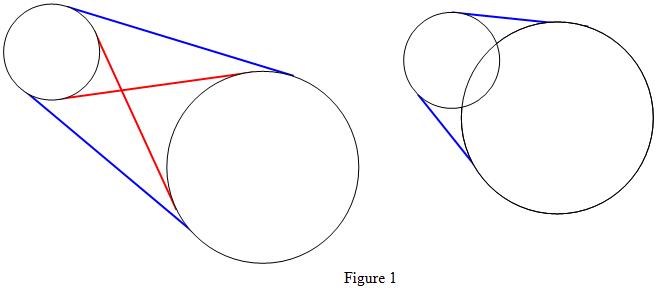
Depending on how two circles are arranged, they can have 0, 2, or 4 tangent lines. If the circles don't intersect, as on the left in Figure 1, they have 4 tangents: 2 outer tangents (blue) and 2 inner tangents (red). If the circles overlap, as shown on the right in Figure 1, they have only 2 outer tangents. If one circle contains the other, they have no tangents.
Suppose the two circles C1 and C2 have radii r1 and r2 where r2 >= r1.
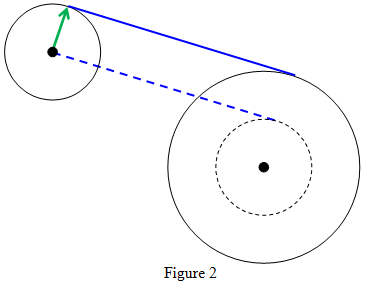
To find the outer tangents, consider Figure 2. The dashed circle has the same center as C2 and radius r2 - r1. By using the example
Find the tangent lines between a point and a circle in Visual Basic 6, you can find the tangent lines between C1's center and this dashed circle. Now move that line perpendicularly to itself distance r1 to get the outer tangent shown in Figure 2. Offset the other point/circle tangent perpendicular to itself to get the other outer tangent.
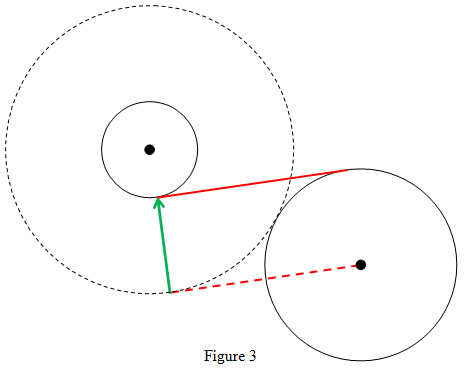
To find the inner tangents, consider Figure 3. Here the dashed circle has the same center as C1 and radius r1 + r2. By again using the example
Find the tangent lines between a point and a circle in Visual Basic 6, you can find the tangent lines between C2's center and this dashed circle. Now move that line perpendicularly to itself distance r2 to get the inner tangent shown in Figure 3. Offset the other point/circle tangent perpendicular to itself to get the other inner tangent.
The basic idea here is somewhat tricky but if you stare long enough at the pictures, you should be able to see how it works. You might also try drawing some pictures of your own.
The FindCircleCircleTangents method shown in the following code uses this technique to find the tangents between two circles.
|
|
' Find the tangent points for these two circles.
' Return the number of tangents: 4, 2, or 0.
Public Function FindCircleCircleTangents( _
ByVal c1 As PointF, ByVal radius1 As Single, ByVal c2 _
As PointF, ByVal radius2 As Single, _
ByRef outer1_p1 As PointF, ByRef outer1_p2 As PointF, _
ByRef outer2_p1 As PointF, ByRef outer2_p2 As PointF, _
ByRef inner1_p1 As PointF, ByRef inner1_p2 As PointF, _
ByRef inner2_p1 As PointF, ByRef inner2_p2 As PointF) _
As Integer
Dim radius2a As Single
Dim v1x As Single
Dim v1y As Single
Dim v1_length As Single
Dim v2x As Single
Dim v2y As Single
Dim v2_length As Single
Dim dx As Single
Dim dy As Single
Dim dist As Double
Dim radius1a As Single
' Make sure radius1 <= radius2.
If (radius1 > radius2) Then
' Call this method switching the circles.
FindCircleCircleTangents = _
FindCircleCircleTangents( _
c2, radius2, c1, radius1, _
outer1_p2, outer1_p1, _
outer2_p2, outer2_p1, _
inner1_p2, inner1_p1, _
inner2_p2, inner2_p1)
Exit Function
End If
' Initialize the return values in case
' some tangents are missing.
Set outer1_p1 = New PointF
Set outer1_p2 = New PointF
Set outer2_p1 = New PointF
Set outer2_p2 = New PointF
Set inner1_p1 = New PointF
Set inner1_p2 = New PointF
Set inner2_p1 = New PointF
Set inner2_p2 = New PointF
' ***************************
' * Find the outer tangents *
' ***************************
radius2a = radius2 - radius1
If (Not FindTangents(c2, radius2a, c1, outer1_p2, _
outer2_p2)) Then
' There are no tangents.
FindCircleCircleTangents = 0
Exit Function
End If
' Get the vector perpendicular to the
' first tangent with length radius1.
v1x = -(outer1_p2.Y - c1.Y)
v1y = outer1_p2.X - c1.X
v1_length = CSng(Sqr(v1x * v1x + v1y * v1y))
v1x = v1x * radius1 / v1_length
v1y = v1y * radius1 / v1_length
' Offset the tangent vector's points.
outer1_p1.X = c1.X + v1x
outer1_p1.Y = c1.Y + v1y
outer1_p2.X = outer1_p2.X + v1x
outer1_p2.Y = outer1_p2.Y + v1y
' Get the vector perpendicular to the
' second tangent with length radius1.
v2x = outer2_p2.Y - c1.Y
v2y = -(outer2_p2.X - c1.X)
v2_length = CSng(Sqr(v2x * v2x + v2y * v2y))
v2x = v2x * radius1 / v2_length
v2y = v2y * radius1 / v2_length
' Offset the tangent vector's points.
outer2_p1.X = c1.X + v2x
outer2_p1.Y = c1.Y + v2y
outer2_p2.X = outer2_p2.X + v2x
outer2_p2.Y = outer2_p2.Y + v2y
' If the circles intersect, then there are no inner
' tangents.
dx = c2.X - c1.X
dy = c2.Y - c1.Y
dist = Sqr(dx * dx + dy * dy)
If (dist <= radius1 + radius2) Then
FindCircleCircleTangents = 2
Exit Function
End If
' ***************************
' * Find the inner tangents *
' ***************************
radius1a = radius1 + radius2
FindTangents c1, radius1a, c2, inner1_p2, inner2_p2
' Get the vector perpendicular to the
' first tangent with length radius2.
v1x = inner1_p2.Y - c2.Y
v1y = -(inner1_p2.X - c2.X)
v1_length = CSng(Sqr(v1x * v1x + v1y * v1y))
v1x = v1x * radius2 / v1_length
v1y = v1y * radius2 / v1_length
' Offset the tangent vector's points.
inner1_p1.X = c2.X + v1x
inner1_p1.Y = c2.Y + v1y
inner1_p2.X = inner1_p2.X + v1x
inner1_p2.Y = inner1_p2.Y + v1y
' Get the vector perpendicular to the
' second tangent with length radius2.
v2x = -(inner2_p2.Y - c2.Y)
v2y = inner2_p2.X - c2.X
v2_length = CSng(Sqr(v2x * v2x + v2y * v2y))
v2x = v2x * radius2 / v2_length
v2y = v2y * radius2 / v2_length
' Offset the tangent vector's points.
inner2_p1.X = c2.X + v2x
inner2_p1.Y = c2.Y + v2y
inner2_p2.X = inner2_p2.X + v2x
inner2_p2.Y = inner2_p2.Y + v2y
FindCircleCircleTangents = 4
End Function
|
|
|
Note that this problem is closely related to the "Belt Problem" where the goal is to calculate the length of a belt needed to connect two pulleys directly (using the outer tangents) or crossed (using the inner tangents). Sometimes the direct (external tangent) version is called the "Pulley Problem."
A couple of definitions:
- An inner tangent is one that intersects the segment joining the circles' centers.
- An outer tangent is one that does not intersect the segment joining the circles' centers.
- The point where the internal tangents intersect is called the internal homeothetic center and it lies along the segment connecting the circles' centers.
- The point where the extensions of the external tangents intersect is called the external homeothetic center and it lies along the segment connecting the circles' centers. If the circles have the same radii, then the external tangents are parallel and the external homeothetic center is at infinity.
|
| |

|
| |
|
|
