The binomial coefficient, written 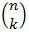 and pronounced "n choose k,"
is the number of ways you can pick k items from a set of n items. For example, suppose you have a deck of 5 cards (n = 5) and you
want to know how many different hands of 3 cards you can make (k = 3). If you number the cards 1 through 5, then the possible combinations are: and pronounced "n choose k,"
is the number of ways you can pick k items from a set of n items. For example, suppose you have a deck of 5 cards (n = 5) and you
want to know how many different hands of 3 cards you can make (k = 3). If you number the cards 1 through 5, then the possible combinations are:
- 1,2,3
- 1,2,4
- 1,2,5
- 1,3,4
- 1,3,5
- 1,4,5
- 2,3,4
- 2,3,5
- 2,4,5
- 3,4,5
That means 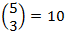 . .
Notice that the selections are unordered. In other words, 1,2,3 is the same as 3,2,1.
In addition to its combinatoric meaning, the binomial coefficient 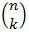 gives the coefficient of the xk term in (1 + x)n.
gives the coefficient of the xk term in (1 + x)n.
The value of the binomial coefficient is easy to calculate using the formula: 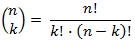 . For example, . For example,
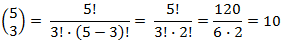
Unfortunately the factorial function grows very quickly so using this formula you can only calculate values for relatively small values of n and k. For example, 28! is too big to fit in Visual Basic's Currency data type so you cannot calculate the binomial coefficient when n > 27.
However, the values on the bottom of the equation are big, too. The two values largely cancel out, leaving a result that is much more manageable. The trick is in calculating the binomial coefficient in a way so the intermediate values don't get too big.
To see how to do this, consider the formula and rearrange it a bit like this:
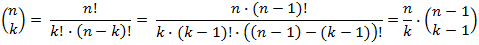
This lets you write "n choose k" in terms of a simple fraction times "n - 1 choose k - 1." If you repeat this process, you represent the original value as a product of simple fractions like this:
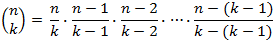
If you group the terms from the right working backwards, you successively calculate:
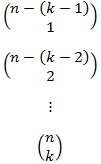
Note that the top value is simply n - (k - 1). Using that value, you can build the others.
Because each of those values represents a binomial coefficient, it must have an integer value. That means you can start with the rightmost term and multiply it by each of the terms to the left, getting an integer result at each step.
Here's the Visual Basic 6 code to perform this calculation.
|
