A convex hull is a smallest convex polygon that surrounds a set of points. If you imagine the points as pegs sticking up in a board, think of a convex hull as a rubberband wrapped around them.
This program demonstrates several useful techniques.
It uses an AngleValue function to order the points. It uses the numeric value dy / (dy + dx) to order the angle from one point to another with respect to the horizontal. This number is not the angle itself, but it has the property that AngleValue(A) < AngleValue(B) if Angle(A) < Angle(B).
The program starts with a point guaranteed to be on the convex hull. For example, the point with the smallest Y coordinate. Then it begins sweeping around to find the point with the smallest AngleValue. It adds that point to the hull and repeats the sweep from the new point starting with the sweep angle it used in the last test. This process continues until the program finds the start point again.
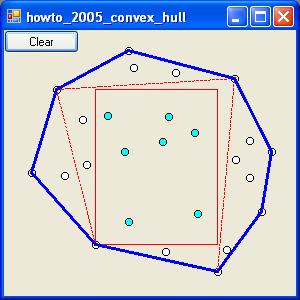
The program also culls some points out to make finding the convex hull faster. To do this, it finds the points that most closely represent the points' upper left, upper right, lower left, and lower right corners. It finds the largest rectangle parallel to the X and Y axes that fits within the quadrilateral defined by those points. This rectangle is guaranteed to lie within the convex hull. The program then removes all points inside this culling rectangle.
To use the program, click several times to select points. Each time you select a point, the program draws the points, highlights those that are culled, draws the culling quadrilateral and rectangle, and draws the convex hull.
For more information on graphics programs in Visual Basic 6, see my book Visual Basic Graphics Programming.
| 
