Sorts of All Types
By Rod Stephens
Sorting is one of the most heavily studied topics in algorithms for several reasons. First, sorting is a common programming task. Allowing a user to sort and view information in different ways makes data more meaningful.
Second, sorting algorithms demonstrate many important algorithmic techniques such as binary subdivision and recursion. Studying these algorithms allows you to hone your programming skills in a relatively simple setting.
Finally, and perhaps most importantly, different sorting algorithms work differently under different circumstances, so no single algorithm is the best choice for all occasions. Understanding which algorithm works best with different sets of data is as important as understanding the algorithms themselves. Only by understanding a variety of algorithms can you pick the one that is right for a given task.
This article describes four sorting algorithms that can handle a wide variety of sorting tasks.
Bubblesort
Bubblesort is without a doubt the most misunderstood sorting algorithm ever invented. Some programmers use bubblesort all the time even though it is usually not the fastest algorithm. Others claim that bubblesort is a bad algorithm that should never be used. As is often the case with such extreme positions, both are wrong.
Bubblesort is a highly specialized algorithm that is useful under only two sets of circumstances. First, if the list of items to be sorted is very short, bubblesort is quite fast. Its method of arranging items by switching them around is very efficient if the list to be sorted contains fewer than 5 or 10 items.
Second, if the items to be sorted are already in mostly sorted order, bubblesort is extremely efficient. If most of the list is randomly arranged, however, bubblesort is abysmally slow. For this reason you must be careful before you use bubblesort.
How Bubblesort Works
Bubblesort scans through a list looking for two adjacent items that are out of order. When it finds two such items, it swaps them. It repeats this process until all of the items are in order.
In the list on the left of Figure 1, the item 34 is out of order. When the algorithm passes through the list, it finds that 34 and 67 are out of order so it switches them. During the second pass, the algorithm sees that the items 65 and 34 are out of order so it switches them. The algorithm continues "bubbling" the item 34 towards the top of the array until it reaches its final position.
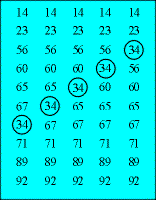
Figure 1. The item 34 bubbles up to its correct position.
This algorithm is faster if it alternates upward and downward passes through the list. During downward passes like the ones illustrated in Figure 1, the item 34 can move only one position upwards. In this example the algorithm requires four passes through the list to move the item to its correct position.
On the other hand, an upward pass through the list would be able to move the item many positions. It would see that 34 and 67 were out of position and switch them. During the same pass, it would then notice that 34 and 65 were out of position so it would switch them, too. It would then switch 34 with 60 and 56, all in one pass.
During each set of upward and downward passes, at least one new item will reach its final position. If the list is initially mostly sorted, the algorithm will need only a few passes through the list to reposition the ones that are out of order.
Figure 2 shows the Delphi source code for the two-way bubblesort algorithm. The Sort program on this month's Companion Disk demonstrates this code.
type
ValueType = Longint; // Type used in the arrays.
IndexType = Longint; // Type used to index arrays.
procedure Bubblesort(var List : array of ValueType;
min, max : IndexType);
var
last_swap, i, j : IndexType;
tmp : ValueType;
begin
// During this loop, min and max are the smallest and largest
// indexes of items that might still be out of order.
// Repeat until we are done.
while (min < max) do
begin
// Bubble up.
last_swap := min - 1;
// for i := min + 1 to max
i := min + 1;
while (i <= max) do
begin
// Find a bubble.
if (List[i - 1] > List[i]) then
begin
// See where to drop the bubble.
tmp := List[i - 1];
j := i;
repeat
List[j - 1] := List[j];
j := j + 1;
if (j > max) then Break;
until (List[j] >= tmp);
List[j - 1] := tmp;
last_swap := j - 1;
i := j + 1;
end else
i := i + 1;
end; // while (i <= max) do.
// End bubbling up.
// Update max.
max := last_swap - 1;
// Bubble down.
last_swap := max + 1;
// for i := max - 1 downto min
i := max - 1;
while (i >= min) do
begin
// Find a bubble.
if (List[i + 1] < List[i]) then
begin
// See where to drop the bubble.
tmp := List[i + 1];
j := i;
repeat
List[j + 1] := List[j];
j := j - 1;
If j < min Then Break;
until (List[j] <= tmp);
List[j + 1] := tmp;
last_swap := j + 1;
i := j - 1;
end else
i := i - 1;
end; // while (i >= min) do
// End bubbling down.
// Update min.
min := last_swap + 1;
end; // while (min < max) do
end;
|
Figure 2. Two-way bubblesort.
Selectionsort
Like bubblesort, selectionsort is efficient for very small lists. It also has the advantage of being extremely simple, so it is easy to implement, debug, and maintain.
The algorithm begins by searching the list for the smallest item. It then swaps that item with the item at the front of the list. Next it searches the remaining items for the next smallest and swaps it into the list's second position. The algorithm continues searching the shrinking list of unsorted items, picking out the smallest, and swapping it to the end of the sorted section at the front of the list. When it has swapped every item into its final position, the algorithm stops. The Delphi code for selectionsort is shown in Figure 3.
procedure Selectionsort(var List : array of ValueType;
min, max : IndexType);
var
i, j, best_j : IndexType;
best_value : ValueType;
begin
for i := min to max - 1 do
begin
best_value := List[i];
best_j := i;
for j := i + 1 to max do
begin
if (List[j] < best_value) Then
begin
best_value := List[j];
best_j := j;
end;
end; // for j := i + 1 to max do
List[best_j] := List[i];
List[i] := best_value;
end; // for i := min to max - 1 do
end;
|
Figure 3. Selectionsort.
Quicksort
The quicksort algorithm uses a recursive divide-and-conquer technique. As long as the list to be sorted has at least two items, the algorithm splits the list in two. It then recursively calls itself to sort the two smaller sublists.
To split a list, the algorithm picks an item from the list to use as a dividing point. It moves all of the items that are smaller than the dividing item to the beginning of the list. It moves the other items to the end of the list. It then calls itself recursively to sort two sublists.
How the algorithm selects the dividing item is critical and there are several approaches it might take. The simplest is to use the first item in the list. If the items are initially arranged randomly, there is a good chance the first item will belong near the middle of the list. When the algorithm uses that item to divide the list, the two smaller lists will have roughly equal size. This makes the sublists grow smaller very quickly so it provides good performance.
On the other hand, if the list is initially sorted, this method produces terrible results. When the algorithm uses the first item to divide the list, it moves all of the other items into the second of the sublists because the dividing item is the smallest item present. The second sublist will contain all of the other items, so the algorithm makes little progress. The algorithm will not only be slow, it will enter a very deep chain of recursion, possibly exhausting the system resources.
A much better method for selecting a dividing element is to pick one randomly. Then no matter how the items are initially arranged, the item will probably not be too near the smallest or largest. When the algorithm divides the list, the two smaller lists will be significantly smaller than the original, so the algorithm will make reasonable progress.
Quicksort suffers from one more special situation. If the list of items contains many duplicates, the algorithm cannot always separate the list into two smaller lists of roughly equal size. For example, if the list holds 100,000 items with values between 1 and 10, the algorithm will quickly reduce the problem to sorting smaller lists containing thousands of identical values. Quicksort handles these trivial lists very inefficiently. The algorithm can be modified to handle this special case, but most programmers simply ignore it. This situation is uncommon and, in any case, it is better handled by the countingsort algorithm described in the next section.
In practice quicksort is extremely fast so it is the sorting algorithm of choice for most programmers. Figure 4 shows the quicksort algorithm's Delphi source code.
procedure Quicksort(var List : array of ValueType;
min, max : IndexType);
var
med_value : ValueType;
hi, lo, i : IndexType;
begin
// If the list has <= 1 element, it's sorted.
if (min >= max) then Exit;
// Pick a dividing item randomly.
i := min + Trunc(Random(max - min + 1));
med_value := List[i];
// Swap it to the front so we can find it easily.
List[i] := List[min];
// Move the items smaller than this into the left
// half of the list. Move the others into the right.
lo := min;
hi := max;
while (True) do
begin
// Look down from hi for a value < med_value.
while (List[hi] >= med_value) do
begin
hi := hi - 1;
if (hi <= lo) then Break;
end;
if (hi <= lo) then
begin
// We're done separating the items.
List[lo] := med_value;
Break;
end;
// Swap the lo and hi values.
List[lo] := List[hi];
// Look up from lo for a value >= med_value.
lo := lo + 1;
while (List[lo] < med_value) do
begin
lo := lo + 1;
if (lo >= hi) then Break;
end;
if (lo >= hi) then
begin
// We're done separating the items.
lo := hi;
List[hi] := med_value;
Break;
end;
// Swap the lo and hi values.
List[hi] := List[lo];
end; // while (True) do
// Sort the two sublists.
Quicksort(List, min, lo - 1);
Quicksort(List, lo + 1, max);
end;
|
Figure 4. Quicksort.
Countingsort
It can be shown that the fastest possible sorting algorithms that use comparisons must take on the order of N * log(N) steps to sort a list of N items. In fact, bubblesort and selectionsort take on the order of N2 steps. Quicksort needs only N * log(N) steps in most cases, though it can use N2 steps in the worst case.
Countingsort does not use comparisons, so it is not restricted by the N * log(N) bound and, under the right circumstances, is much faster than the others.
On the other hand, countingsort only works under very specific circumstances. First, the items being sorted must be integers. It is difficult to sort strings using countingsort. Second, the items' values must range over a relatively limited set of values. If values range from 1 to 1,000, countingsort will give good results. If values range from 1 to 2 billion, countingsort will be slow and most computers do not have enough memory to make it work at all.
Countingsort begins by creating a temporary array with bounds that cover the range of items in the list. If the items range in value from 1 to 1,000, the algorithm creates an array with bounds between 1 and 1,000.
Since Delphi does not allow a program to dynamically resize arrays, the example program declares the counts variable to be a pointer to an array containing 100 million entries. It then uses GetMem to allocate space for the counts array as shown in the following code fragment.
type
TCountArray = array[0..100000000] of IndexType;
PCountArray = ^TCountArray;
// Code omitted...
counts : PCountArray;
GetMem(counts, (max_value - min_value + 1) * SizeOf(IndexType));
|
The algorithm then examines each item in the list and increments the counts array entry for the item's value. For instance, if an item has value 12, the algorithm adds one to counts(12). When this stage is finished, counts(i) holds the number of items in the list that have the value i.
The program can then read out the sorted list. It gives the first counts(min_value) items the value min_value. It gives the next counts(min_value + 1) items the value min_value + 1. It continues through the list assigning values until it has completely filled the sorted list.
To sort N items that span a range of M values, countingsort uses roughly 2 * N + M steps. First, it uses M steps to initialize the counts array entries to zero. Next, it uses N steps looking through the list to count the item values. It then uses N more steps to fill in the sorted list entries.
If N is large and M is small, 2 * N + M is much smaller than N * log(N). For example, suppose a list contains 1 million numbers with values between 1 and 1,000. Then N * log(N) is roughly 20 million while 2 * N + M is only about 2 million.
Lists like this one are particularly troublesome for quicksort since they contain many duplicate values. In one test on a 166 MHz Pentium, quicksort took 15 seconds to sort this list while countingsort took only 0.15 seconds--one hundredth as long.
Figure 5 shows the Delphi source code for countingsort.
procedure Countingsort(var List, SortedList : array of ValueType;
min, max : IndexType; min_value, max_value : ValueType);
var
i, j, next_index : IndexType;
count_index : ValueType;
counts : PCountArray;
begin
// Create the Counts array.
GetMem(counts, (max_value - min_value + 1) * SizeOf(IndexType));
// Initialize the counts to zero.
for i := 0 to max_value - min_value do
counts[i] := 0;
// Count the items.
for i := min to max do
begin
count_index := List[i] - min_value;
counts[count_index] := counts[count_index] + 1;
end;
// Place the items in the sorted array.
next_index := min;
for i := min_value to max_value do
begin
for j := 1 to counts[i - min_value] do
begin
SortedList[next_index] := i;
next_index := next_index + 1;
end;
end;
// Free the memory allocated for the counts array.
FreeMem(counts);
end;
|
Figure 5. Countingsort.
Summary
Every sorting algorithm has its strengths and weaknesses. Bubblesort is fast for large lists that are almost sorted, but slow for others. Selectionsort is easy to program and fast for small lists, but it is painfully slow for large lists. Quicksort is fast most of the time, but has trouble if the list contains many duplicate values. Finally, countingsort only works with integers that span a small range of values, but for those lists it is unbeatable.
Here is a checklist that can help you pick the algorithm that is right for your situation.
- If the list is more than 99 percent sorted, use bubblesort.
- If the list is very small, use bubblesort or selectionsort.
- If the list contains integers with a small range or values, use countingsort.
- Otherwise use quicksort.
Chose your algorithm wisely and one of these four will provide you with excellent performance under almost any circumstances.
Downloads
Download a 5K zip file containing the example program described in this article. This program demonstrates the bubblesort, selectionsort, quicksort, and countingsort algorithms.
|
This article originally appeared in the January 1998 issue of
Delphi Informant
magazine. If you like the article, visit the magazine's Web
site to see if you would like to subscribe.
|
| 



